Models of Elliptical Galaxies in 1-1-1 Resonances
with Axial and Discrete Symmetries.
Ferrer S.(1), Palacian J.(2), San Juan J.F.(3), Yanguas P.(4)
(1) Grupo de Mecanica Espacial, Univ. de Zaragoza, 50009 Zaragoza, Spain,
(2) Departamento de Matematica e Informatica, Univ. Publica de Navarra, 31006 Pamplona, Spain
(3) Departamento de Matematicas y Computacion,
Univ. de La Rioja, 26004 Logrono, Spain,
(4) Departamento de Matematica e Informatica,
Univ. Publica de Navarra, 31006 Pamplona, Spain
The composition of the Whittaker transformation with a Lissajous
transformation in the instantaneous trajectory plane, opens the possibility
to normalize 3 dimensions perturbed isotropic harmonic oscillators in
a 1-1-1 resonance.
In this way we manage to achieve an extension of the studies involving
solutions in the equatorial and meridian planes, by
now considering orbits at any inclination. A main feature of this
transformation is the expression of the unperturbed Hamiltonian
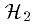 as proportional to one of the momentum coordinates; thus, when the
perturbation is periodic, the solution of the equation that has to be
solved in each step of the normalization process is simply an average with
respect to the elliptic anomaly
as proportional to one of the momentum coordinates; thus, when the
perturbation is periodic, the solution of the equation that has to be
solved in each step of the normalization process is simply an average with
respect to the elliptic anomaly 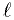 . Recognizing the fact that, from the Lissajous normalization and
the axial symmetry, the doubly reduced orbit space is S², we introduce
coordinates which allow to look for relative equilibria and their
bifurcations over the domain of parameters.
. Recognizing the fact that, from the Lissajous normalization and
the axial symmetry, the doubly reduced orbit space is S², we introduce
coordinates which allow to look for relative equilibria and their
bifurcations over the domain of parameters.
As a first application
we deal with 2-DOF cubic and quartic polynomial potentials with axial and
discrete symmetries proposed by de Zeeuw. In particular we deal with the relation between degenerate
cases of the averaged system with the integrable cases of the full
problem. As far as we know only first order studies have been done; we
have extended the normalization up to higher orders.
As an example, dealing solely with the cubic perturbation, we extend
the study done by Miller for the meridian case. As a second application we apply the concept of the elimination of
the parallax and radial simplifications to perturbed isotropic oscillators.
References
-
[1]
-
Abad, A. and San Juan, J. F.: 1994, PSPC: A Poisson Series Processor
coded in C, in Dynamics and Astrometry of Natural and Artificial
Celestial Bodies, Eds. K. Kurzynska et al., Astron. Observ.
University of Poznan, Poland, 383--389.
-
[2]
-
Deprit, A.: 1981, Celes. Mech. 24, 111-153.
-
[3]
-
Deprit, A.: 1991, Celes. Mech. & Dynam. Astron. 51, 201-226;
Deprit, A., Elipe A.: Idem, 227-250; Miller, B. R.: Idem, 251-270.
-
[4]
-
de Zeeuw, T.: 1985, Motion in the core of a triaxial potential,
M.N.R.A.S. 215, 731--760.
-
[5]
-
de Zeeuw, T. and Franx, M.: 1991, Structure and dynamics of elliptical
galaxies, Annu. Rev. Astron. Astrophys. 29, 239--74.
-
[6]
-
Ferrer, S., and Garate, A.: 1995, to appear in
Hamiltonian Systems and Celestial Mechanics,
Ed. E. A. Lacomba and J. Llibre, Advances Series in
Nonlinear Dynamics, World Scientific, Singapore.
-
[7]
-
Ferrer, S., Lara, M., Palacian, J. and Yanguas, P.: 1995, to appear in
Proceedings of NATO-ASI Hamiltonian Systems with three or more degrees
of freedom, S'Agaro, Eds. A. Delshams et al.
-
[8]
-
Fradkin D. M.: 1965, Three-dimensional isotropic harmonic oscillator and SU_3,
Am. J. Phys. A 33, 207--211.
-
[9]
-
Pascua, P., Rubio J.L., Viartola, A. and Ferrer, S.: 1995,
to appear in Int. J. of Bifur. & Chaos.
-
[10]
-
Yanguas, P.: Thesis, in preparation.
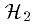 as proportional to one of the momentum coordinates; thus, when the
perturbation is periodic, the solution of the equation that has to be
solved in each step of the normalization process is simply an average with
respect to the elliptic anomaly
as proportional to one of the momentum coordinates; thus, when the
perturbation is periodic, the solution of the equation that has to be
solved in each step of the normalization process is simply an average with
respect to the elliptic anomaly 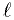 . Recognizing the fact that, from the Lissajous normalization and
the axial symmetry, the doubly reduced orbit space is S², we introduce
coordinates which allow to look for relative equilibria and their
bifurcations over the domain of parameters.
. Recognizing the fact that, from the Lissajous normalization and
the axial symmetry, the doubly reduced orbit space is S², we introduce
coordinates which allow to look for relative equilibria and their
bifurcations over the domain of parameters.