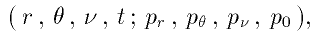
Grupo de Mecanica Celeste, Departamento de Matematica Aplicada a la
Ingenieria,
E. T. S. de Ingenieros Industriales, Universidad de Valladolid,
E - 47 011 Valladolid, Spain.
Numerous attempts have been made to reduce perturbed Kepler problems into the form of perturbed linear oscillators. We will consider the framework of Linear and Regular Celestial Mechanics to bring the equations of motion into linear form by giving them the form corresponding to a 4--dimensional harmonic oscillator. A general reference for this subject could be Stiefel & Scheifele (1971). More recently, Deprit et al. (1994) have refined the approach and put the question in a more rigorous context.
Burdet (1969) investigated the linearization of the Kepler problem in focal variables, which can be interpreted as homogeneous Cartesian coordinates in a projective space. They were made canonical by Ferrandiz, in completing the coordinates with the respective momenta (Ferrandiz 1988 and 1991, and references therein; Deprit et al. 1994, §§ 4.4; Elipe et al. 1995) so as to obtain eight redundant variables of focal type, the so--called BF variables, in terms of which the equations of motion are similar to those of Burdet. To sum up, the BF variables reduce the pure Kepler problem to four harmonic oscillators.
Let H_0 denote the standard Keplerian Hamiltonian. Conditions for linearization of the equations of motion derived from perturbed Kepler Hamiltonian problems, formulated in homogeneous canonical formalism, will be analyzed. Our study will allow us to decide on potentials admitting exact reduction to oscillators.
In the 8--dimensional phase space, we start from a model of perturbation in extended Hill--Whittaker variables,
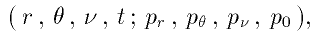
in which the perturbing potential is proportional to a power of the inverse of the distance, the coefficient being some function of canonical momenta that can also be expanded in powers of a small parameter:
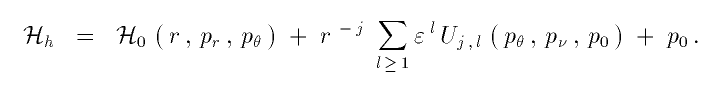
Some radial intermediary Hamiltonians occurring in Artificial Satellite Theory (Deprit 1981, p. 138 and p. 141; Alfriend & Coffey 1984; Floria 1993, § 7) fit into this pattern.
We will follow a variant of the focal method canonical treatment of Ferrandiz § Fernandez--Ferreiros (1991). If Burdet--Ferrandiz focal--type variables are used, and a true--like anomaly (introduced by a generalized Sundman transformation) is the independent variable, we show that the only
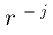
perturbation which is exactly linearized by our variant of the focal method is just that given by the Deprit--like and Alfriend--Coffey Hamiltonians (Deprit, 1981, p. 138; Alfriend & Coffey 1984.) This conclusion does not preclude the possibility of approximate reduction to oscillator form (equations of motion corresponding to non--linearly perturbed harmonic oscillators), with non--linear terms of the order of the perturbation, when dealing with other potentials, in which case we give formulae for the calculation of such non--linear contributions.
These results emphasize some reasons for the limitations and failure of an application of the focal method to obtain linearization of perturbed two--body problems.
Key words: linearization, perturbed Kepler Hamiltonian systems, BF focal variables, canonical transformations, time transformation, radial intermediaries, zonal satellite.