Hamiltonian of N--Body Problem as a
D'Alembertian function
Kholshevnikov K.V.
Astronomical Institute, St. Petersburg University,
Stary Peterhof, 198904 St.Petersburg, Russia.
E-mail: kvk@aispbu.spb.su
The well--known D'Alembertian characteristic of disturbing and other
important for Celestial Mechanics functions means a property of Fourier
series coefficients, permitting to replace it by a Maclaurin series in
terms of
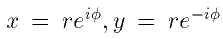 ,
,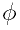 being an angular variable, r-- action one
(e.g. eccentricity or inclination).
We show that such a coefficients property is a consequence of a
functional one. Namely, introduce a notion of D'Alembertian functions
which are holomorph and limited in a domain
being an angular variable, r-- action one
(e.g. eccentricity or inclination).
We show that such a coefficients property is a consequence of a
functional one. Namely, introduce a notion of D'Alembertian functions
which are holomorph and limited in a domain
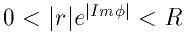 and are invariant under the transformation
and are invariant under the transformation
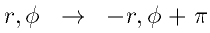 .
Such a domain may be represented like a bottle with infinitely
long and infinitely thin neck.
.
Such a domain may be represented like a bottle with infinitely
long and infinitely thin neck.
Of course a D'Alembertian function possesses a D'Alembertian
characteristic, moreover we can estimate the coefficients, the size
of convergence domain and the function itself.
Simpliest example. Cartesian coordinates of a planet in elliptic
motion are D'Alembertian functions with respect to two pairs:
sine of semi--inclination -- longitude of ascending node; eccentricity --
mean anomaly. In the first case R = 1, in the second
R = 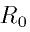 , where
, where 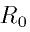 = 0.662743
is the famous Laplace limit .
Note, that attainability of
= 0.662743
is the famous Laplace limit .
Note, that attainability of 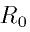 is rather unexpected.
Recently (IAU symposium 172, Paris, 1995) I have claimed that to reach
it we ought
to introduce a complicated asymmetrical bottle instead of a simple one
above.
is rather unexpected.
Recently (IAU symposium 172, Paris, 1995) I have claimed that to reach
it we ought
to introduce a complicated asymmetrical bottle instead of a simple one
above.
Hamiltonian of Planetary Problem. Consider Hamiltonian function
of Planetary N--Body Problem in heliocentric or Jacobian coordinate
system. Then it represents a D'Alembertian function with respect to
above mentioned pairs for each planet. The corresponding values
of R are less than ones in Two Body Problem due to collisions in a
complex
domain. If two orbits intersect really after proper turning of lines
of nodes and/or apsides than corresponding R = 0. In other words
the D'Alembertian property disappears. In the Solar System such is
the Neptune --- Pluto case.
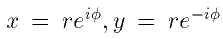 ,
,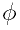 being an angular variable, r-- action one
(e.g. eccentricity or inclination).
We show that such a coefficients property is a consequence of a
functional one. Namely, introduce a notion of D'Alembertian functions
which are holomorph and limited in a domain
being an angular variable, r-- action one
(e.g. eccentricity or inclination).
We show that such a coefficients property is a consequence of a
functional one. Namely, introduce a notion of D'Alembertian functions
which are holomorph and limited in a domain
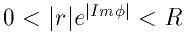 and are invariant under the transformation
and are invariant under the transformation
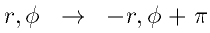 .
Such a domain may be represented like a bottle with infinitely
long and infinitely thin neck.
.
Such a domain may be represented like a bottle with infinitely
long and infinitely thin neck.
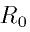 , where
, where